7 Graphs

1. A directed graph whose nodes (vertices) are of type alpha can be represented as

   type graph(alpha) == set(alpha X alpha);
   

   Each pair 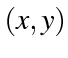$(x,y)$ in the set represents an edge from $x$ to $y$.
   
   What does the following function do?:

   f: graph(alpha) -> set(alpha);
   f(G) <= if G=empty
           then empty
           else let ((a,b),G1) == choose(G)
                in (a & (b & empty)) U f(G1);
   

2. Write a function:

   outdegree: alpha X graph(alpha) -> num;
   

   which returns the out-degree of a particular vertex in the graph.
3. Write a function nexts which, given a vertex $v$ and a graph $g$ finds the set of vertices that are at the end of an out-going edge from $v$.

4. Given a function

   cfp: alpha -> graph(alpha) -> set(list(alpha));
   

   which is such that cfp x g is the set of all cycle-free paths from x in g, write a function

          reachable: alpha X graph(alpha) -> set(alpha);
   

   such that reachable(x, g) is the set of all vertices reachable from x in g. (You may need to define some extra functions.)
5. Using cfp, write a function for finding the length of the shortest path between two vertices in a graph. (You may need to define some extra functions. )